1. 有损陷门函数
一个简单但重要的观察: 现代多媒体压缩技术可以对无损的多媒体(如视频、音频)进行大幅压缩, 得到有损的多媒体, 而人眼/人耳难以感知无损与有损之间的差异. 比如, 你的肉眼能观察出两幅图像的差异么?

无损: 250kb

有损: 250kb
Chris Peikert和Brent Waters见微知著, 提出了有损陷门函数(Lossy Trapdoor Functions) [PW08]. 简言之, 有损陷门函数的生成算法具有双重模式, 正常模式生成单射可逆的函数, 有损模式生成信息损失的函数(像在信息论意义下丢失了原像大部分信息), 两种类型的函数在计算意义下不可区分.
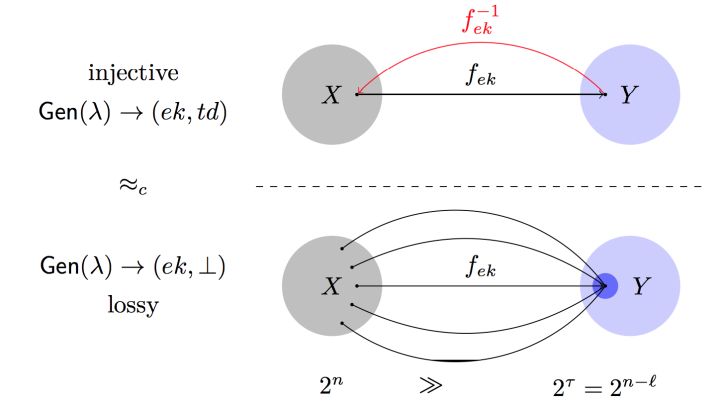
两种类型的函数在外形上相似, 但信息论意义下表现迥异. 正是这种巨大的反差使得有损陷门函数的威力无穷. 以下依次介绍如何构造和如何应用.
2. 如何构造
核武器威力无穷, 但前提是能造出来. 构造有损陷门函数的技术难点在于保证两种统计行为迥异的函数在计算意义下不可区分. 我们分别介绍具体构造和通用构造.
2.1 具体构造
Peikert和Waters给出了矩阵式构造方法: (1) 函数的原像空间为 维向量空间, 每个原像都是一个维向量; (2) 函数索引(evaluation key)为矩阵, 函数的定义为:
我们来格物致知, 理解矩阵式构造的精巧之处:
- 密钥生成算法在正常模式下输出为单位矩阵的“加密”作为 , 输出“加密”中的解密密钥作为陷门; 在信息损失模式下输出低秩矩阵(如全零阵 )的“加密”作为 . “加密”的安全性保证了两种类型的函数在计算意义下不可区分.
- 本质上定义了一个维向量空间上的线性映射,计算输入的函数值可以理解为对进行线性变换. 在正常模式下满秩, 因此是单射, 并且可以利用陷门高效求逆, 求逆方式可以非正式地理解为线性方程组求逆; 在信息损失模式下, 非满秩, 将维的原像空间映射到维的像空间, 其中. 函数的像在信息论意义下丢失了部分原像的信息.
善于思考的读者应该能体会到矩阵式构造的必然性: 输入=向量、函数索引=线性变换的设计使得我们能够灵活控制函数的统计行为.
在矩阵式构造的框架下, 我们可以基于大整数分解类问题、离散对数类困难问题和格中的困难问题给出有损陷门函数的具体构造.
2.1 通用构造
有损陷门函数的函数索引具备单射可逆和信息损失这两种计算不可区分形式, 哈希证明系统中哈希函数 的输入可以划分为Yes实例和No实例, 同样计算不可区分. 科学无巧合, Hoeteck Wee敏锐地指出对偶哈希证明系统蕴含有损陷门函数[Wee12], 构造如下:
上述构造的精要之处是密钥和输入的对换技术: 将哈希证明系统中的密钥 作为函数的输入, 将的输入作为函数的索引.
- 当为No实例时, 对偶哈希证明系统的性质保证单射可逆; 当为Yes实例时,投射性保证了的值由惟一确定, 因此信息有损.
- No实例和Yes实例的计算不可区分性保证了单射可逆模式和信息损失模式的计算不可区分性.
上述构造建立了两大密码组件之间的内在关联, 充分体现了Wee的研究风格: 深优美.
3. 损有何用
3.1 应用套路—损盈转换
与哈希证明系统相似, 大部分基于有损陷门函数的密码方案设计采用三步走模式:

- 单射可逆模式用于密码方案构造, 保证功能性.
- 信息有损模式建立密码方案在信息论意义下的安全性
此处的直观是将待保护的消息作为函数的输入, 因为信息丢失, 所以拥有无穷计算能力的敌手也无法从函数的输出中恢复消息).
- 单射可逆模式和有损模式的计算不可区分性最终建立密码方案在计算意义下的安全性.
3.2 重要应用
有损陷门函数的重要应用包括但远不限于:
- 单向陷门函数
突破性意义在于 (i)任意随机性提取器都可以作为hardcore functions, 提取线性长度的hardcore bits; (ii) 首次给出基于离散对数类问题和格中困难问题的单射单向陷门函数构造, 之前所有的单向陷门函数构造均基于大整数分解类假设.
- 强安全性的单向陷门函数: 包括相关积单向陷门函数和自适应单向陷门函数.
- 公钥加密: 借鉴Naor-Yung的双重加密的思想, 基于有损陷门函数及其扩展给出了精巧的CCA-secure PKE的黑盒构造
突破性意义在于 (i)构造具备randomness recovering的特性, 开辟了获得CCA安全的新途径; (ii) 首次基于格中困难问题的给出标准模型下的CCA-secure PKE.
- 简洁高效的伪随机数发生器、抗碰撞哈希函数、不经意传输协议、有损加密、确定性公钥加密等.
3.3 扩展
有损陷门函数还有诸多衍生和变化

- All-But-Many有损陷门函数
有损分支的数量从1提升到任意多项式规模, 在SO-CCA PKE的构造中具有重要的应用.
- 极度有损函数 [Zha16]
细心的读者可能很早就思考这样一个问题, 有损模式下函数究竟能有多损? 令像集的大小为r , 根据生日攻击, 敌手总能在\sqrt{r} 的时间内以较大的概率找到碰撞, 进而区分单射可逆模式和有损模式. 显然, 如果``太损'', 如r是多项式规模, 那么相应的有损函数并不能对所有多项式能力的敌手安全, 无法适配主流的黑盒/一致归约技术.
Zhandry偏偏爱上了这匹野马, 他提出了极度有损函数的概念, 即在有损模式下, 函数的像集可以塌缩到多项式级别. 那么如何驾驭极度有损陷门函数呢? 答案是非黑盒/个体归约技术: 只要归约算法知道敌手运行时间的上界 , 那么它可以将有损模式下函数像集大小设定为大于 以超越生日界, 保证单射模式和有损模式的不可区分性. 极度有损函数的重要应用是实例化random oracle, 美中不足的是目前还没有基于常规假设的构造.
邓神在最近的开创性工作中系统发展了非黑盒/个体归约技术, 有兴趣的读者请看[Den2017].
- 规则有损函数 [CQX2018]
有损陷门函数的功能太过强大, 这也导致它的效率不佳. 我们发现在一些应用中陷门可逆的性质并不必要, 甚至单射性也不是必要的. 根据这一观察, 我们提出了规则有损函数, 即正常模式下的函数不必是单射可逆的, 仅需映射规则. 该泛化带来了两大优势: (1) 在矩阵式构造框架下, 相比有损陷门函数, 规则有损函数的索引尺寸大幅缩减, 计算效率成倍提升; (2) 任意哈希证明系统均蕴含规则有损函数. 在应用方面, 我们展示了规则有损函数在抗泄漏密码学中的强力应用, 给出了泄漏率最优的单向函数、一次消息验证码和(基于身份)密钥封装方案.
